Conversion of the Gamebook Adventures system to a 2D6 system

This article is even more esoteric than yesterday’s topic on probabilities in the Gamebook Adventures system, but it’s related and to those that are designing and writing gamebooks of their own, this may prove useful for their own designs…

Or at least give them ideas. There’s a few things happening in the “gamebook world” at the moment that could benefit from this, and so having done this conversion for a new project I’m working on, I thought I’d share my work, and to kinda follow on from my article yesterday.

In a nutshell, I’ve converted the “standard” Gamebook Adventures system to something that is easy to manage in “old school” pencil-and-paper format, retains the aspects of Offence, Defence and Fitness, and yet doesn’t require keeping track of a lot of dice.

I’ll start with the final result of this conversion; the OFF/DEF matrix that is used to determine required rolls in combat; and then explain back from that as to just why I came up with the numbers I did:

                      

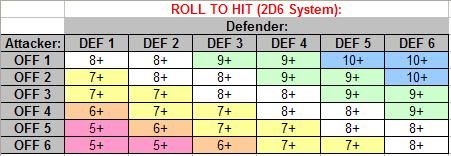
I like numbers… And the patterns and behaviours that can emerge in them. And this table to me, at the moment anyway, is beautiful. :)

But let’s take a number of steps back, to “first principles” if you like. I began with the convention that (as in the Gamebook Adventures system and most other gamebook systems) you have a turn-based combat that is primarily one individual or side versus another, where the two sides take it in turns to make “rolls to hit”.

For simplicity, I simply made this “roll to hit” a roll of a certain number or greater on two six-sided dice. If you hit, then you do a set amount of damage, depending on the weapon used. (Many other gamebook systems have used similar simple mechanics).

I based the simplified system on using two six-sided dice because:

• “Normal” dice are easy to come by.

• Having no more than two dice for any roll makes it easy to count.

• Using two dice rather than one die, means that your possible outcomes are skewed towards the middle of the range.

The last one needs a bit more explanation. If you base a scale on the roll of a single die, then the odds of each possible result are the same, and you get a linear scale of progression where the relevant battle stats (in this case the Offence and Defence values) increase or decrease at a constant rate. Progression is an important consideration in game design (and could spawn an article all of its own), but I’ll just say that I think it is desirable to build in exponential decline into your system, such that increases have a progressively smaller effect. Otherwise, the system is prone to “power creep” where to remain challenging, everything has to keep scaling up… I could go on elaborating this point, (shit, I’ve written post-grad papers on statistical distributions in the past) but then I think we’d get more than a little off topic haha.

On this 2D6 scale, I set a baseline value of 8+ to hit. This is so that it broadly follows the convention that the “hitting and missing have a similar likelihood, all else being equal”, and so that your chance to hit increases up the scale (by going from 8+ to 7+ to 6+ etc) and decreases down the scale (by going from 8+ to 9+ to 10+ etc) by a decreasing amount.

If you’re still reading this, congratulations! -I think it gets easier from here… What I did next is take the “to hit” probabilities I’d calculated for the GA system, and found the nearest probability for each combination on a 2D6 scale, to end up with this:
                     

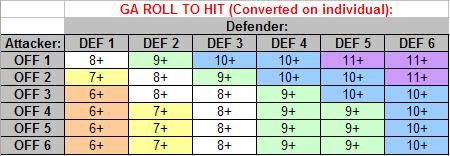
…Which I didn’t like so much; it was too hard to hit at higher DEF ratings, and there was no difference at higher OFF ratings (taking the closest probability on a 2D6 scale).

So I “fiddled” with the numbers a bit to even out the changes and have a differentiated scale to get to this:
                      

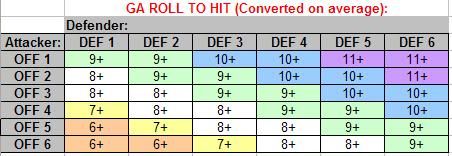
Which I then re-calibrated back to the 8+ baseline I’d decided on (if OFF and DEF are equal then your chance to hit is 8+) to get back to the table at the start of this article.

Damages inflicted was based on the average damage per round values I’d calculated for each OFF value in the GA system, giving a rough rule of thumb that your attack did 4 times the OFF value when it hit. Then I arbitrarily decided to halve these damage values (and halve the corresponding Vitality values) so that you inflicted only twice your Offence rating when you hit (e.g. you do 2 dam per hit at OFF 1, 4 dam at OFF 2 etc), with the option to have some exceptions too.

Fitness checks in attack would simply add 1 to your roll to hit, or deduct 1 from your opponent’s roll to hit, keeping the odds in a “nice range” where nothing becomes too likely or unlikely, and viola!

So I’ll leave you with the following charts, showing the probabilities for the Gamebook Adventures, with and without the Fitness bonus, compared against the 2D6 conversion, with and without the Fitness bonus. Hopefully, you’ll see that the scales are comparable:
                

                

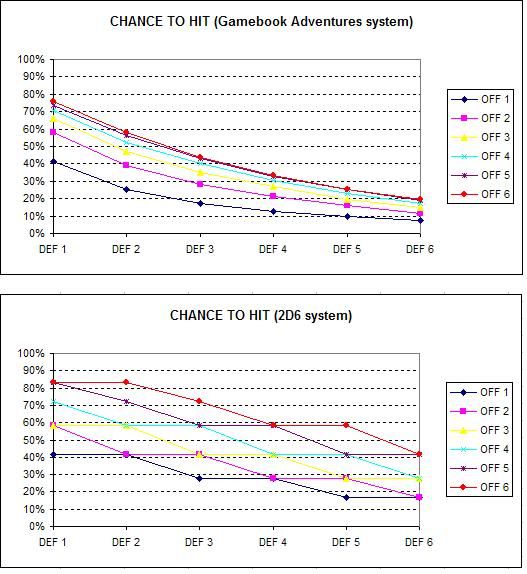
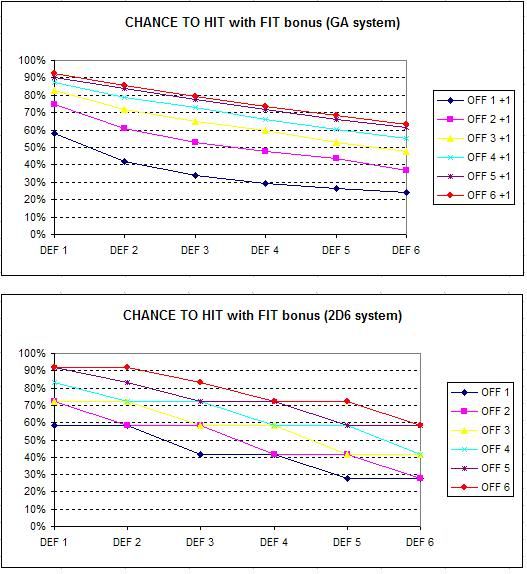
Okay now seriously, I think I should stop this blog binge on stats now already! :)