Probabilities in the Gamebook Adventures system

Today’s article is all about probabilities in the Gamebook Adventures system (with some limited comparison to other systems, particularly Fighting Fantasy). Statistics can be a bit of a dry topic haha, so I’ll try to reduce it to the important elements for you… Well important that is if you’re writing for such a system or are interested to know what the game odds are… Beware though, there’s a lot of tables and charts incoming :)

Calculating probabilities for a system such as Fighting Fantasy is reasonably straight forward: (In a typical battle) you roll two six-sided dice for each combatant and add a given Skill score to each combatant’s roll, with the highest score dealing 2 Stamina damage to the other combatant. Use of Luck rolls makes it a little more complicated but not by much. You can “Test your Luck”; by attempting to roll two dice equal to or under your current Luck; in order to do one more Stamina damage, but failing this roll means you do one less Stamina. Skill and Luck scores vary, resulting in an exponential scale where even a few points of Skill difference make it unlikely for one side to win, even with far more Stamina.

For example, if your Skill is 3 lower than your opponent’s, then your opponent is roughly five times more likely than you are, to be the one making a hit in a given combat round, not including the Luck factor. In other words, if your hero has Skill 9 Stamina 24 and your opponent Skill 12 Stamina 5, then you both have about the same chance of winning…

The Gamebook Adventures system is considerably more complicated to calculate probabilities for (even though the rules themselves are of a similar level of complexity) and shares a similar but less extreme exponential scale, such that the outcome of a combat is not as much of a sure thing. Combatants roll between one and six six-sided dice to attack (as determined by their Offence rating) and between one and six six-sided dice to defend (as determined by their Defence rating). If the attacker’s highest roll is higher than the defender’s highest roll, then they do damage equal to the sum of all their dice. (And in the case of tied rolls, the two tied dice are removed and the next two highest rolls are compared, until no dice are left). In addition, the hero can make a “Fitness check” on any given combat round by rolling two dice under their current Fitness. This is similar to “Testing your Luck” in the Fighting Fantasy system, except that the advantage given is to add 1 to their highest roll, significantly increasing the chance of hitting or defending.

In the extreme case of 6 dice in Offence against an opponent with 6 dice in Defence, and including the two additional dice rolled for a Fitness check, there are 6^14 possible dice combinations for any given round (that’s 78,364,164,096 combinations). And to calculate the highest roll and damage inflicted for each of these combinations, is quite a task… But I’ve done this (well kind of; I had to take some short cuts, but the end conclusions are about the same) and this is what I present below.

This isn’t meant to be a rigorous statistics paper, so I’ll spare you comprehensive details of how I came up with these numbers… But basically I listed every dice combination out on a spreadsheet, so that I could be sure I was calculating correct averages etc, until the number of possible combinations became too unwieldy. I listed all combinations up to seven dice, which is 6^7 or 279,936 combinations. The numbers for the remaining eight to fourteen dice combinations I estimated using a “best fit” exponential regression equation. In other words, I took the half-finished set of values I had manually calculated and used them to apply a formula to estimate the rest…

First of all, we’ll ignore the impact of Fitness checks, and just focus on the chance of success (success being an attack that hits the defender) for each Offence / Defence combination:

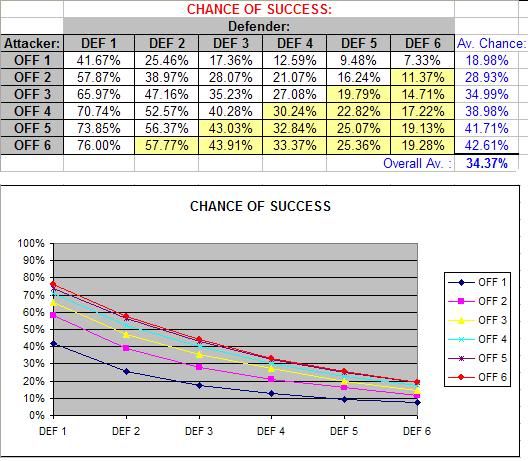
So to interpret what these numbers mean, it’s saying that if your Offence value was 6, and your opponent had a Defence value of 1, then (not including Fitness checks) your chance of success (i.e. hitting) is 76.00%, and if their Defence was 2, your chance is *about* 57.77% and so on…

The yellow cells in the above table are where I had to cut corners as the number of combinations was too large to individually analyse. These are the values I extrapolated based on the trend already shown. This trend (as you can see in the above graph) is an exponential decline, where the degree to which your chances drop lessens as Defence values increase.

Here are some interesting conclusions from these numbers:

• Even at maximum Offence (6) versus minimum Defence (1), you have at best a 76% chance of hitting. This compares to a 100% chance for a similarly extreme matchup in the Fighting Fantasy system, and to many other dice-based game systems where the best odds tend to be 95% (anything but a roll of one on a twenty-sided dice), 97% (anything but double-one or double-six on two six-sided dice) or 99% in percentile-based systems.

• Conversely though, even at minimum Offence (1) versus maximum Defence (6), you still have a 7.33% chance of hitting (more once you consider Fitness checks), which typically compares to between 0% and 5% in other systems.

• Typically your chance of hitting; without including Fitness checks; is lower in the Gamebook Adventures system than that for other systems such as Fighting Fantasy, Lone Wolf, Dungeons and Dragons and the Basic Role Playing system. (However when you do hit, your damage is typically higher than what occurs in these systems).

• Increasing Offence or Defence has an increasingly smaller impact. For instance, you’ll see that Offence 6 is only slightly better than Offence 5, particularly against high Defence values. (Although I suspect it’s not quite a close as shown, since the values in the yellow cells were those obtained from extrapolation).

Now let’s look at the average damage inflicted when you hit:

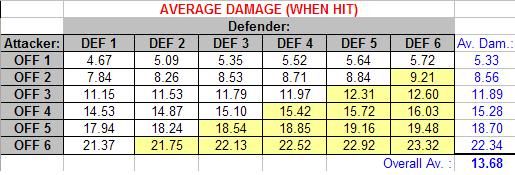
It’s actually difficult to draw much from these numbers since you need to factor in the chance of hitting to say how much damage is done on average each round… The amount of damage done for any given Offence rating only increases slightly with increasing Defence (based on the fact that the higher the Defence value you’re trying to hit, the more likely that a successful hit was based on a high roll).

By multiplying the chance to hit, by the average damage done when hit, we come to this table (which is very useful from a design / game-balancing point of view):

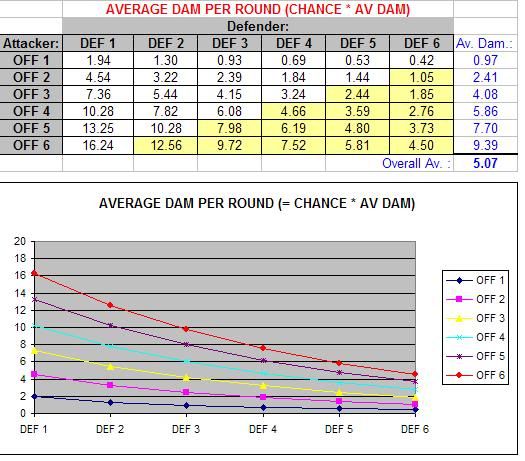
So now we can start to see exactly how hard any given combat is. For instance, if you have an Offence of 4 and a Defence of 2, and are fighting an enemy with an Offence and Defence value of 3, then you inflict an average of 6.08 damage per attack, whilst your opponent inflicts an average of 5.44 damage per attack… Pretty useful huh?

However, as useful as this is, it doesn’t take into account Fitness checks that you can make during battle. Which is what I’ll now cover, (briefly as it gets pretty complicated haha). For the purposes of this analysis I’ve assumed that Fitness checks are only used to add 1 to the highest attack roll, but they can be used to add 1 to your highest defence roll too. –I’ve assumed that using Fitness checks to add to your highest defence roll (instead of highest attack roll) is typically a “weaker” strategy, considering a defensive strategy just prolongs the battle rather than finishes it.

There are a few things to consider when calculating the benefit of Fitness checks. We need to consider that your Fitness is generally between 7 and 12, and that with each Fitness check made in combat (where they need to roll 2D6 under their current Fitness to be successful), your current Fitness is reduced by one. We also need to consider that if the Fitness check is successful, you add 1 to your highest roll, and if unsuccessful you deduct 1 from your highest roll.

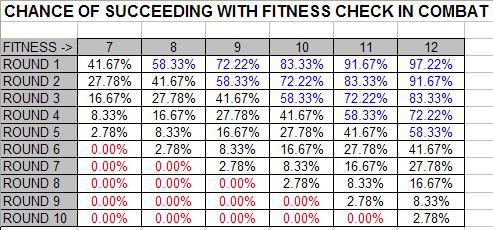
The blue numbers in the table above are where your odds of succeeding on the Fitness check are greater than 50%, and the red numbers are where your Fitness has become so low that a Fitness check has no chance of succeeding. The above numbers are relatively simple to calculate (a 2D6 Fitness check only has 36 combinations) and basically what it boils down to is that if your current Fitness is 7 or less, you’re more likely to fail than succeed (so unless you fancy your dexterity to “nudge the dice a bit”, you’re better off not trying Fitness checks). –Also note that the figures in the above table, assume that you’re making a Fitness check on every round (with your Fitness being reduced by one each time).

So how much difference does having a +1 on your highest roll make? A lot. You may be surprised just how much:

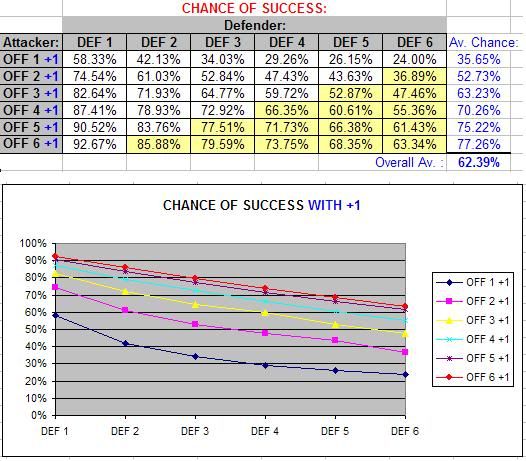
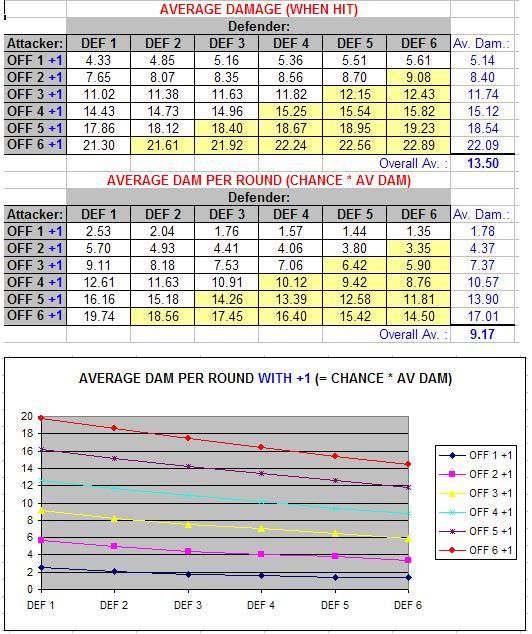
Now you’re quite possibly reeling from “numbers overload” so I’ll try to distil all of this down for you into the following two charts which show how much a successful Fitness check increases your odds of hitting by and how much it increases your average damage per round:

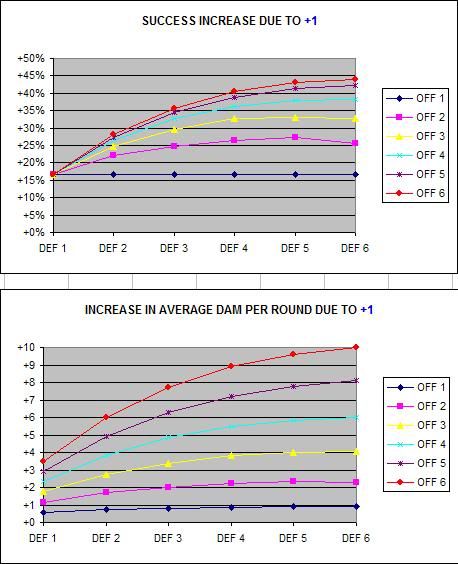
Note that because some of these numbers are based on extrapolation, they don’t exactly follow what the real trend would be (Offence 2 versus Defence 6 stands out as looking a little bit wrong), but you get the idea… Well maybe you do if I haven’t lost you in a sea of tables and charts ;)

I’ve got one more table to show you, and this is the “master table” that I use to balance out battles in the Gamebook Adventures system. Since I originally crunched out this table, Ben Britten has a developed an amazing Gamebook Adventures tool that will simulate and statistically summarise ten of thousands of runs of a given combat at the click of a mouse; giving you a report on the average number of rounds a given combat lasted, average damage inflicted/dealt, percentage wins etc; but this table can be used if you don’t have access to that ;) (And yes the numbers match!)

The table below, gives you the average amount of damage done per round for each Offence/Defence combination after taking into account Fitness checks. For “simplicity”, I have used a Fitness value of 10: 

The red numbers indicate cases where the benefit of a successful Fitness check is outweighed by the risk of the Fitness check failing; i.e. the average damage dealt per round is actually less than if you didn’t make a Fitness check at all. In other words, when the opponent’s Defence is low, you’re actually better off not risking a Fitness check to add 1 to your highest Offence roll (remembering that a failed Fitness check deducts from, instead of adds to, your highest dice roll).

I use the above table to work out how much damage is done and received on average per round, including assuming that the hero is using Fitness checks to help them attack, (until their Fitness has dropped to 7 in which case they’re better off not making them at all). This then gives me an estimate of who will win, how many rounds it will take, and how much damage they'll suffer in the process.

Some conclusions on the Fitness bonus:

• The Fitness bonus typically almost doubles your chance to hit and the average amount of damage you can expect to do in a given round.

• Another way of stating the effect of the Fitness bonus is that any attack with OFF 2 or more and the +1 Fitness bonus is, on average, more likely to hit than even an OFF 6 attack without the +1 Fitness bonus.

• The Fitness bonus also alleviates the "scalability problem" which otherwise leads to significantly longer battles the higher DEF values go, even if OFF values increase as well. Without this bonus, you have a situation where an OFF 1 attack versus a DEF 1 defence has a 42% chance of success, but an OFF 6 attack versus a DEF 6 defence has only a 19% chance of success. With the +1 fitness bonus, an OFF 1 attack versus a DEF 1 defence has a 58% chance of success, and an OFF 6 attack versus a DEF 6 defence has a 63% chance of success.

…I had actually meant to write more on a similar topic; a statistical conversion of the Gamebook Adventures system to a purely 2D6 system; but I’ll leave that for another blog. Surely I’ve given you enough stats, tables and charts for one day ;)