
Today’s article is all about probabilities in the Gamebook Adventures system (with some limited comparison to other systems, particularly Fighting Fantasy). Statistics can be a bit of a dry topic haha, so I’ll try to reduce it to the important elements for you… Well important that is if you’re writing for such a system or are interested to know what the game odds are… Beware though, there’s a lot of tables and charts incoming :)
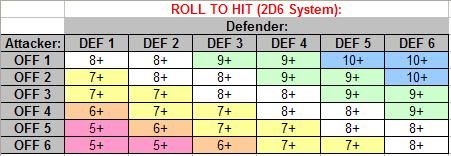
Calculating probabilities for a system such as Fighting Fantasy is reasonably straight forward: (In a typical battle) you roll two six-sided dice for each combatant and add a given Skill score to each combatant’s roll, with the highest score dealing 2 Stamina damage to the other combatant. Use of Luck rolls makes it a little more complicated but not by much. You can “Test your Luck”; by attempting to roll two dice equal to or under your current Luck; in order to do one more Stamina damage, but failing this roll means you do one less Stamina. Skill and Luck scores vary, resulting in an exponential scale where even a few points of Skill difference make it unlikely for one side to win, even with far more Stamina.
For example, if your Skill is 3 lower than your opponent’s, then your opponent is roughly five times more likely than you are, to be the one making a hit in a given combat round, not including the Luck factor. In other words, if your hero has Skill 9 Stamina 24 and your opponent Skill 12 Stamina 5, then you both have about the same chance of winning…
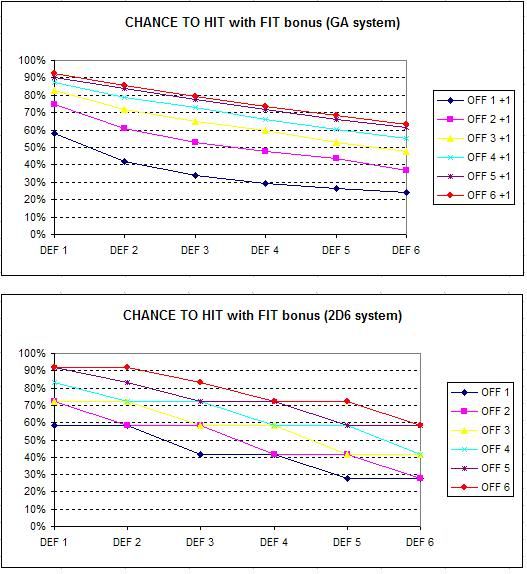
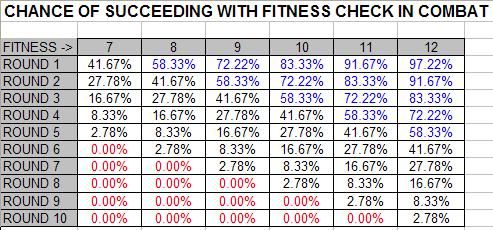
The Gamebook Adventures system is considerably more complicated to calculate probabilities for (even though the rules themselves are of a similar level of complexity) and shares a similar but less extreme exponential scale, such that the outcome of a combat is not as much of a sure thing. Combatants roll between one and six six-sided dice to attack (as determined by their Offence rating) and between one and six six-sided dice to defend (as determined by their Defence rating). If the attacker’s highest roll is higher than the defender’s highest roll, then they do damage equal to the sum of all their dice. (And in the case of tied rolls, the two tied dice are removed and the next two highest rolls are compared, until no dice are left). In addition, the hero can make a “Fitness check” on any given combat round by rolling two dice under their current Fitness. This is similar to “Testing your Luck” in the Fighting Fantasy system, except that the advantage given is to add 1 to their highest roll, significantly increasing the chance of hitting or defending.
In the extreme case of 6 dice in Offence against an opponent with 6 dice in Defence, and including the two additional dice rolled for a Fitness check, there are 6^14 possible dice combinations for any given round (that’s 78,364,164,096 combinations). And to calculate the highest roll and damage inflicted for each of these combinations, is quite a task… But I’ve done this (well kind of; I had to take some short cuts, but the end conclusions are about the same) and this is what I present below.
This isn’t meant to be a rigorous statistics paper, so I’ll spare you comprehensive details of how I came up with these numbers… But basically I listed every dice combination out on a spreadsheet, so that I could be sure I was calculating correct averages etc, until the number of possible combinations became too unwieldy. I listed all combinations up to seven dice, which is 6^7 or 279,936 combinations. The numbers for the remaining eight to fourteen dice combinations I estimated using a “best fit” exponential regression equation. In other words, I took the half-finished set of values I had manually calculated and used them to apply a formula to estimate the rest…
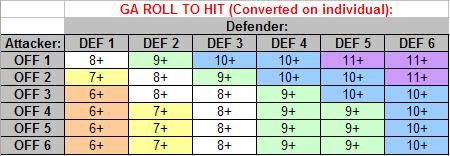
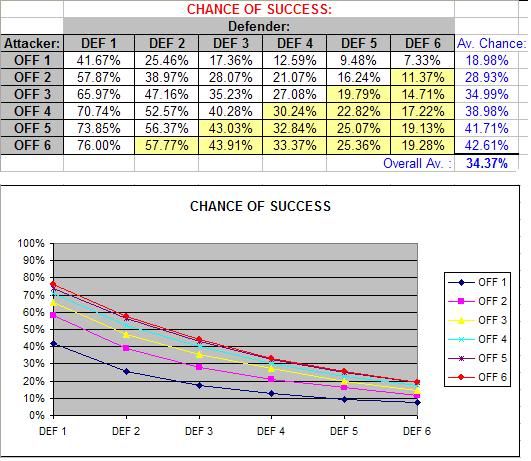
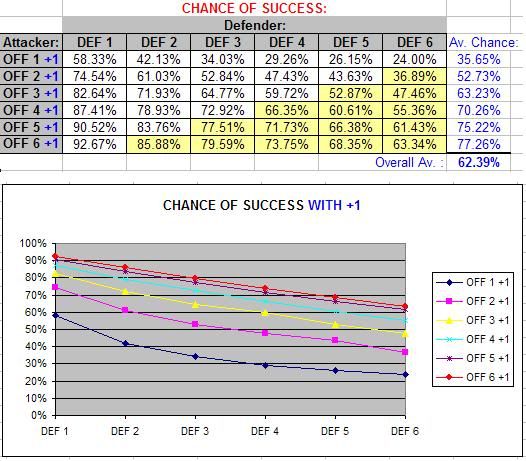
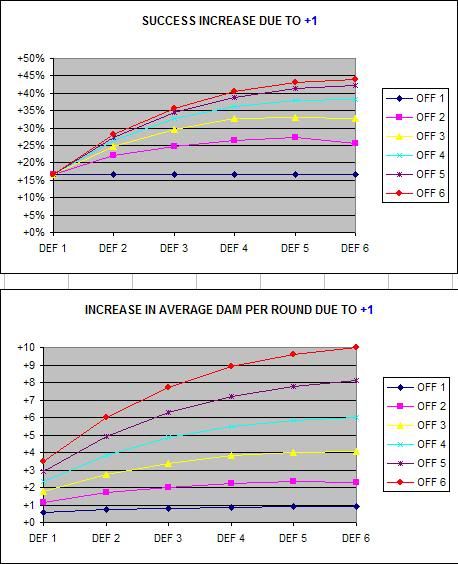
First of all, we’ll ignore the impact of Fitness checks, and just focus on the chance of success (success being an attack that hits the defender) for each Offence / Defence combination:
So to interpret what these numbers mean, it’s saying that if your Offence value was 6, and your opponent had a Defence value of 1, then (not including Fitness checks) your chance of success (i.e. hitting) is 76.00%, and if their Defence was 2, your chance is *about* 57.77% and so on…
The yellow cells in the above table are where I had to cut corners as the number of combinations was too large to individually analyse. These are the values I extrapolated based on the trend already shown. This trend (as you can see in the above graph) is an exponential decline, where the degree to which your chances drop lessens as Defence values increase.
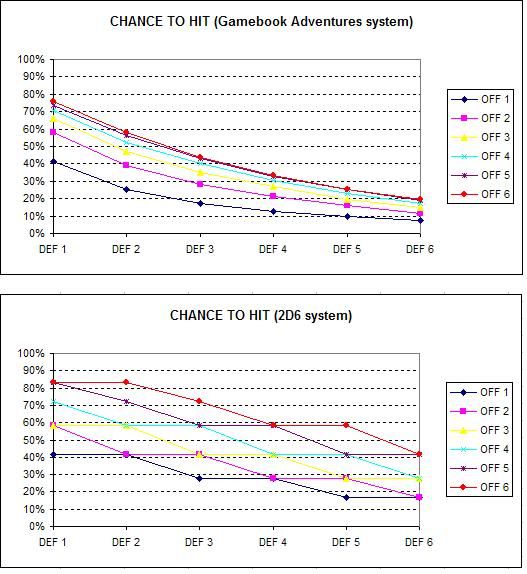
Here are some interesting conclusions from these numbers:
- Even at maximum Offence (6) versus minimum Defence (1), you have at best a 76% chance of hitting. This compares to a 100% chance for a similarly extreme matchup in the Fighting Fantasy system, and to many other dice-based game systems where the best odds tend to be 95% (anything but a roll of one on a twenty-sided dice), 97% (anything but double-one or double-six on two six-sided dice) or 99% in percentile-based systems.
- Conversely though, even at minimum Offence (1) versus maximum Defence (6), you still have a 7.33% chance of hitting (more once you consider Fitness checks), which typically compares to between 0% and 5% in other systems.
- Typically your chance of hitting; without including Fitness checks; is lower in the Gamebook Adventures system than that for other systems such as Fighting Fantasy, Lone Wolf, Dungeons and Dragons and the Basic Role Playing system. (However when you do hit, your damage is typically higher than what occurs in these systems).
- Increasing Offence or Defence has an increasingly smaller impact. For instance, you’ll see that Offence 6 is only slightly better than Offence 5, particularly against high Defence values. (Although I suspect it’s not quite a close as shown, since the values in the yellow cells were those obtained from extrapolation).
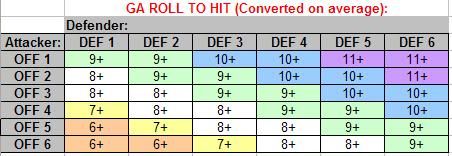
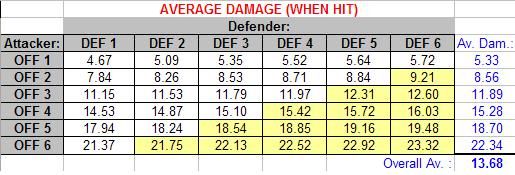
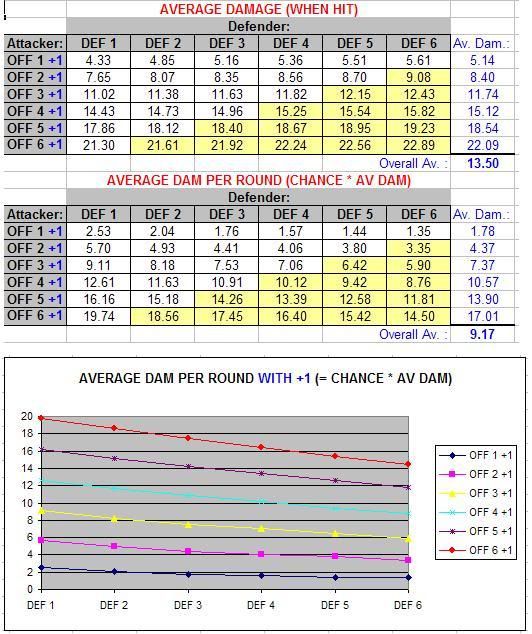
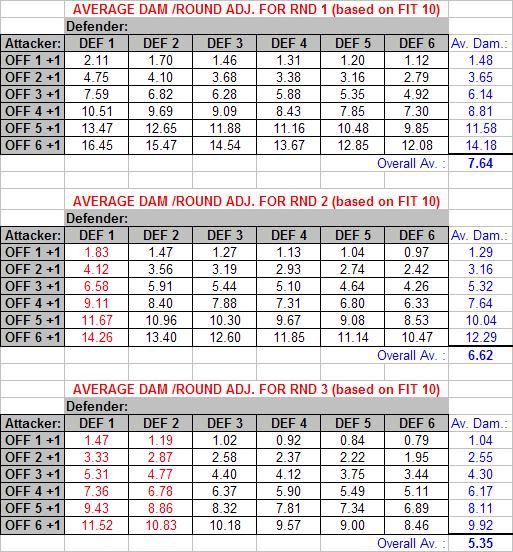
Now let’s look at the average damage inflicted when you hit:
It’s actually difficult to draw much from these numbers since you need to factor in the chance of hitting to say how much damage is done on average each round… The amount of damage done for any given Offence rating only increases slightly with increasing Defence (based on the fact that the higher the Defence value you’re trying to hit, the more likely that a successful hit was based on a high roll).
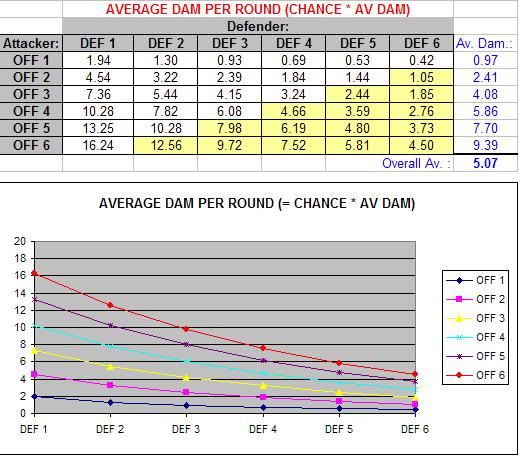
By multiplying the chance to hit, by the average damage done when hit, we come to this table (which is very useful from a design / game-balancing point of view):
So now we can start to see exactly how hard any given combat is. For instance, if you have an Offence of 4 and a Defence of 2, and are fighting an enemy with an Offence and Defence value of 3, then you inflict an average of 6.08 damage per attack, whilst your opponent inflicts an average of 5.44 damage per attack… Pretty useful huh?